서론
ADsP Part 3. 5장 정형 데이터 마이닝 (인공 신경망 분석, 군집분석, 연관분석) 정리
1. 인공 신경망 분석
뉴런의 활성화 함수
- 시그모이드 함수 (로지스틱 회귀분석과 유사)
: 0 ~ 1 사이의 확률값을 가진다

- ReLU 함수
: 0이하 = 0, 0보다 크면 x
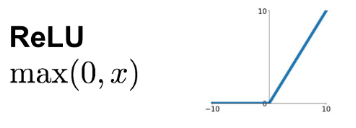
2. 군집분석
- 각 객체(대상)의 유사성을 측정하여 유사성이 높은 대상 집단을 분류하고,
군집에 속한 객체들의 유사성과 서로 다른 군집에 속한 객체간의 상이성을 규명하는 분석 방법
거리
- 군집분석에서 관측 데이터 간 유사성이나 근접성을 측정해 어느 군집으로 묶을 수 있는지 판단하기 위해 거리 사용
연속형 변수
- 유클리디안 거리 (Euclidean Distance)
: 통계적 개념이 내포되어 있지 않아 변수들의 산포 정도가 전혀 감안되어 있지 않았다. - 표준화 거리 (Statistical Distance)
: 해당 변수의 표준편차로 척도 변환한 후 유클리디안 거리를 계산하는 방법
(표준화하면 척도의 차이, 분산의 차이로 인한 왜곡을 피할 수 있다.) - 마하라노비스 거리 (Mahalanobis Distance)
: 통계적 개념이 포함된 거리, 변수들의 산포를 고려하여 이를 표준화한 거리이다.
(그룹에 대한 사전 지식없이는 표본공분산 S를 계산할 수 없으므로 사용하기 곤란) - 맨하탄 거리 (Manhattan Distance)
- 체비셰프 거리
- 캔버라 거리
- 민코우스키 거리
유클리드 거리 (제곱)

맨하탄 거리 (절댓값)

범주형 변수
- 자카드 거리
- 자카드 계수
- 코사인 거리
- 코사인 유사도
: 두 개체의 벡터 내적의 코사인 값을 이용하여 측정된 벡터간의 유사한 정도이다.
코사인 유사도가 1 => 유사도가 높다.
코사이 유사도가 -1 => 유사도가 낮다.
계층적 군집분석
- N개의 군집으로 시작해 점차 군집의 개수를 줄여나가는 방법
최단연결법 (Single Linkage)
- N * N 거리행렬에서 거리가 가장 가까운 데이터를 묶어서 군집을 형성한다.
- 군집과 군집 또는 데이터와 거리를 계산 시 최단거리를 거리로 계산하여 거리 행렬 수정을 진행한다.
- 수정된 거리행렬에서 거리가 가까운 데이터 또는 군집을 새로운 군집으로 형성
최장연결법 (Complete Linkage)
- 군집과 군집 또는 데이터와 거리를 계산 시 최장거리를 거리로 계산하여 거리 행렬 수정을 진행한다.
평균연결법 (Average Linkage)
- 군집과 군집 또는 데이터와 거리를 계산 시 평균을 거리로 계산하여 거리 행렬 수정을 진행한다.
와드연결법 (Ward Linkage)
- 군집내 편차들의 제곱합을 고려한 방법
- 군집 간 정보의 손실을 최소화하기 위해 군집화를 진행
예시) 최단, 최장, 평균 연결법
| x | y | |
| a | 1 | 4 |
| b | 2 | 1 |
| c | 4 | 6 |
| d | 4 | 3 |
| e | 5 | 1 |
Step 1) 거리행렬 계산 (유클리드 거리 사용)
| a | b | c | d | |
| a | ||||
| b | 10 | |||
| c | 13 | 29 | ||
| d | 10 | 8 | 9 | |
| e | 25 | 9 | 26 | 5 |
가장 가까운 d와 e를 한 군집으로 한다.
Step 2_1) 최단연결법
| a | b | c | |
| a | |||
| b | 10 | ||
| c | 13 | 29 | |
| de | 10 | 8 | 9 |
최단연결법은 군집내 가장 가까운 데이터와의 거리를 거리로 계산한다.
b(2,1)과 d(4,3)의 거리 = 8, b(2,1)과 e(5,1)의 거리 = 9 둘 중 더 작은 것 = 8
Step 2_2) 최장연결법
| a | b | c | |
| a | |||
| b | 10 | ||
| c | 13 | 29 | |
| de | 25 | 9 | 26 |
최장연결법은 군집내 가장 먼 데이터와의 거리를 거리로 계산한다.
b(2,1)과 d(4,3)의 거리 = 8, b(2,1)과 e(5,1)의 거리 = 9 둘 중 더 큰 것 = 9
Step 2_3) 평균연결법
| a | b | c | |
| a | |||
| b | 10 | ||
| c | 13 | 29 | |
| de | 17.5 | 8.5 | 17.5 |
평균연결법은 군집내 평균값의 거리를 거리로 계산한다.
b(2,1)과 d(4,3)의 거리 = 8, b(2,1)과 e(5,1)의 거리 = 9 둘의 평균 = 8.5
군집 수 결정

덴드로그램에서 Height값에 따라 군집수를 선택한다.
Height = 1500 (군집 2개)

Height = 500 (군집 3개)

비계층적 군집분석
- N개의 개체를 K개의 군집으로 나눌 수 있는 모든 가능한 방법을 점검해 최적화한 군집을 형성하는 것
K-평균 군집분석 (K-Means-Clustering)
- 주어진 데이터를 K개의 클러스터로 묶는 알고리즘으로, 각 클러스터와 거리 차이의 분산을 최소화하는 방식으로 동작
과정
- 원하는 군집의 개수와 초기값(Seed) 설정하여 Seed 중심으로 군집을 형성
- 각 데이터를 거리가 가장 가까운 Seed가 있는 군집으로 분류
- 각 군집의 Seed값을 다시 계산 (각 군집의 평균을 다시 계산)
- 모든 개체가 군집으로 할당될 때 까지 위 과정 반복
특징
- 연속형 변수에 활용이 가능하다.
- K개의 초기 중심값은 임의로 선택이 가능하다. (가능한 멀리 떨어지는 것이 바람직)
- 초기 중심값의 선정에 따라 결과가 달라질 수 있다.
- 탐욕적 알고리즘으로 안정된 군집은 보장하지만, 최적이라는 보장은 없다.
혼합 분포 군집
- 모형 기반의 군집방법
- 데이터가 K개의 모수적 모형의 가중합으로 표현되는 모집단 모형으로부터 나왔다는 가정하에서
모수와 함게 가중치를 자료로부터 추정하는 방법을 사용 - 혼합모형에서의 모수와 가중치의 추정에는 EM알고리즘 사용
특징
- K-평균 군집의 절차와 유사하지만 확률분포를 도입하여 군집을 수행
- 군집의 크기가 너무 작으면 추정의 정도가 떨어지거나 어려울 수 있다.
- K-평균 군집과 같이 이상치 자료에 민감하다.
EM (Expectataion - Maximization) 알고리즘
- E-단계 : 잠재변수 Z의 기대치 계산
- M-단계 : 잠재변수 Z의 기대치를 이용하여 파라미터를 추정
SOM (Self Organizing Map)
- 자기 조직화 지도 (SOM) 는 비지도 신경망으로 고차원의 데이터를
이해하기 쉬운 저차원의 뉴런으로 정렬하여 지도의 형태로 형상화 한다.

입력층 (Input Layer : 입력벡터를 받는 층)
- 입력변수의 개수와 같은 뉴런 수가 존재
- 입력층의 자료는 학습을 통하여 경쟁층에 정렬되는데, 이를 지도라고 한다.
- 입력층과 경쟁층의 뉴런들은 완전연결 되어 있다.
경쟁층 (Competitive Layer : 2차원 격자로 구성된 층)
- 입력벡터의 특성에 따라 벡터가 한점으로 클러스터링 되는 층
- SOM은 경쟁학습으로 각각의 뉴런이 입력벡터와 얼마나 가까운가를 계산하여
연결강도를 반복적으로 재조정하여 학습한다. - 위의 과정을 거치며 연결강도는 입력 패턴과 가장 유사한 경쟁층 뉴런이 승리자가 된다.
3. 연관분석
- 연관성 분석은 서열분석, 장바구니분석이라고 불린다.
- 연관규칙의 형태 : 조건과 반응의 형태 (if-then)로 이루어져 있다.
연관규칙의 측도
- 지지도 (Support)
: 전체 거래 중 항목 A와 항목 B를 동시에 포함하는 거래의 비율로 정의

- 신뢰도 (Confidence)
: 항목 A를 포함한 거래 중에서 항목 A와 항목 B가 같이 포함될 확률이다. => P(B | A)
(연관성의 정도를 파악할 수 있다.)

- 향상도 (Lift)
: A가 구매되지 않았을 때 품목 B의 구매확률에 비해 A가 구매됐을 때 품목 B의 구매확률의 증가 비
연관규칙 A→B는 품목 A와 품목 B의 구매가 서로 관련이 없는 경우에 향상도가 1이 된다.

4. 기타
나이브 베이즈 분류
- 나이브 베이즈 분류는 데이터에서 변수들에 대한 조건부 독립을 가정하는 알고리즘으로
클래스에 대한 사전 정보와 데이터로부터 추출된 정보를 결합하고 베이즈 정리를 이용하여
어떤 데이터가 특정 클래스에 속하는지를 분류하는 알고리즘
군집모형 평가지표
- 던 지수 (Dunn Index) : 군집간 거리의 최솟값을 분자, 군집 내 욧간 거리의 최댓값을 분모로 하는 지표로
DI 값이 클수록 군집이 잘 이루어진 것으로 볼 수 있음
'자격증 > ADsP' 카테고리의 다른 글
| [ADsP] 38회 합격 후기 (0) | 2023.10.03 |
|---|---|
| [ADsP] 3과목 - 5장 (1,2,3절) (0) | 2023.08.14 |
| [ADsP] 3과목 - 4장 (4,5,6 절) (시계열 분석) (0) | 2023.08.13 |
| [ADsP] 3과목 - 4장 (3절 : 회귀분석) (0) | 2023.08.12 |
| [ADsP] 3과목 - 4장(1,2절) (0) | 2023.08.11 |
