[백준] BOJ 1041 주사위 (골드 5)

문제

---

https://www.acmicpc.net/problem/1041

1041: 주사위

---

해설

---

---

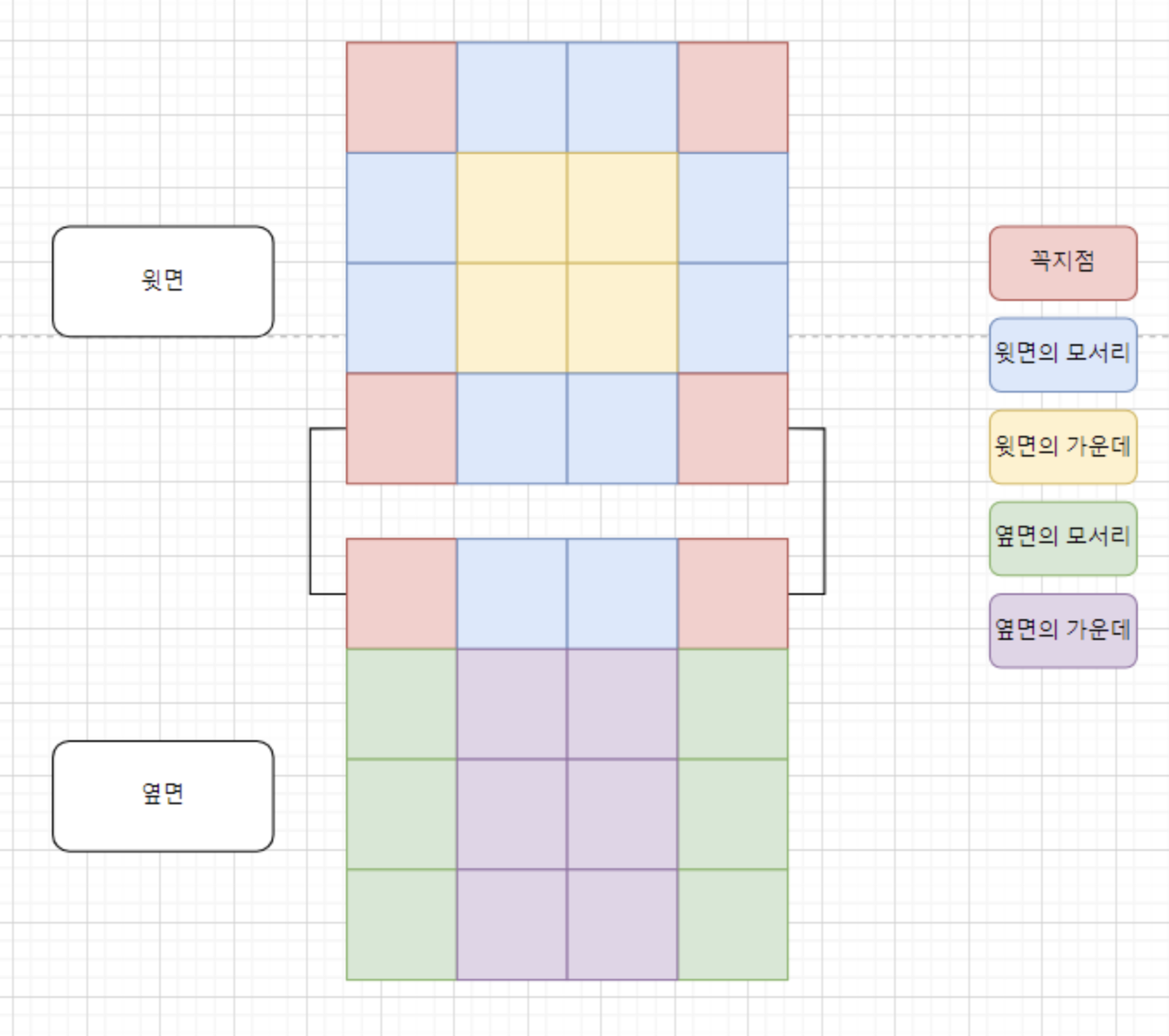
1. 주사위는 기본적으로 반대편 면을 제외하고는 닿아있다.
2. 주사위를 어떻게든 회전시키거나 해서 모든 면의 합을 최소로 만들어야 한다.
3. 이때 케이스를 여러가지로 나눠서 각각의 최소를 구해준다.
   • 케이스 1. 정육면체의 위 꼭지점 (4개)
     • 정육면체의 꼭지점은 3개의 면이 보여져야 한다.
     • 따라서, 3면이 나올 수 있는 조합들 중 최솟값을 하나 찾아서 이를 4개의 꼭지점이므로 * 4를 해서 더한다.
   • 케이스 2. 정육면체의 위 모서리 (꼭지점 제외)
     • 꼭지점을 제외한 모서리 부분은 2개의 면이 보여야 한다.
     • 이때, 윗면은 꼭지점을 제외한 개수만큼 사용된다.
     • 즉 N = 4이면, N - 2(꼭지점 2개를 뺀 개수) * 4개의 모서리 이다.
     • 따라서 2면이 나올 수 있는 조합들 중 최솟값을 찾아서 이를 모든 윗면 모서리에 적용한 개수를 더한다.
   • 케이스 3. 정육면체의 옆 모서리 (꼭지점 제외)
     • 꼭지점을 제외한 모서리 부분은 케이스2와 동일하다.
     • 하지만 아래면은 꼭지점으로 취급하지 않으므로 위의 꼭지점 개수인 1만 빼준다.
     • 즉, N - 1 * 4개
   • 케이스 4. 가운데 직, 정사각형
     • 윗면의 경우 N * N의 외곽을 모두 지우면 N - 1 * N - 1의 정사각형이 된다.
       (위의 케이스 들에 의해 이미 구해진 값이므로 가운데만 구하면 된다.)
     • 옆면의 경우 높이의 경우 맨 위 모서리만 제외하며, 옆면의 경우 양쪽 모서리를 빼줘야하므로 N - 1 * N - 2 * 4
       (4개의 면이므로)
   • 이렇게 구한 모든 케이스의 값을 더해준다.
4. 하지만, 이때 N = 1인 케이스를 커버하지 못하므로
   N = 1일때는 주사위의 값을 모두 더하고 최대값만 빼주면 5개의 면을 최소로 채울 수 있다.

---

코드 (구현)

---

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class BOJ1041 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        StringTokenizer st = new StringTokenizer(br.readLine());
        //
        long[] arr = new long[6];

        long min = Integer.MAX_VALUE;
        for (int i = 0; i < 6; i++) {
            arr[i] = Long.parseLong(st.nextToken());
            min = Math.min(min, arr[i]);
        }
        /**
         * 총 N * 5개의 수를 선택해야 함
         * 꼭지점은 3면의 합이 최소인 경우를 골라야함
         * 경우의 수 (4개 : 맨 위 꼭지점 4개)
         * A, B, D (0, 1, 3)
         * A, B, C (0, 1, 2)
         * A, E, C (0, 4, 2)
         * A, E, D (0, 4, 3)
         * B, D, F (1, 3, 5)
         * B, C, F (1, 2, 5)
         * F, E, D (5, 4, 3)
         * F, E, C (5, 4, 2)
         */
        /**
         * 꼭지 점 제외 두 면을 사용하는 끝은 2개의 면의 합이 최소인 것을 골라야함
         * N - 2개 * 8 (모든 모서리 - 꼭지점 : 4)
         * A, (B, C, D, E) 0, (1,2,3,4)
         * B, (C, D, F) 1, (2, 3, 5)
         * C, (E, F) 2, (4, 5)
         * D, (E, F) 3, (4, 5)
         * E, F (4, 5)
         */
        long res = getMin(arr, min, N);
        System.out.println(res);
    }

    private static long getMin(long[] arr, long min, int N) {
        if(N == 1){
            long sum = 0;
            long max = 0;
            for (int i = 0; i < 6; i++) {
                sum += arr[i];
                max = Math.max(max, arr[i]);
            }
            return sum - max;
        }
        //3개의 면의 합이 최소인 것 : 꼭지점은 3개의 면이 필요함.
        long[] cases1 = {
                arr[0] + arr[1] + arr[2],
                arr[0] + arr[1] + arr[3],
                arr[0] + arr[2] + arr[4],
                arr[0] + arr[3] + arr[4],
                arr[1] + arr[2] + arr[5],
                arr[1] + arr[3] + arr[5],
                arr[2] + arr[4] + arr[5],
                arr[3] + arr[4] + arr[5]
        };
        Arrays.sort(cases1);

        //2개의 면의 합이 최소인 것 : 모서리는 두개의 면이 필요함.
        long[] cases2 = {
                arr[0] + arr[1],
                arr[0] + arr[2],
                arr[0] + arr[3],
                arr[0] + arr[4],
                arr[1] + arr[2],
                arr[1] + arr[3],
                arr[1] + arr[5],
                arr[2] + arr[4],
                arr[2] + arr[5],
                arr[3] + arr[4],
                arr[3] + arr[5],
                arr[4] + arr[5],
        };
        Arrays.sort(cases2);
        long res = min * (N - 2) * (N - 2); // 윗면의 모서리, 꼭지점 제외 최소로 채운 값 (정사각형)
        res += min * 4 * (N - 1) * (N - 2); // 옆면 4개의 모서리, 꼭지점 제외 최소로 채운 값 (직사각형)
        res += cases1[0] * 4; // 꼭지점
        res += cases2[0] * (N - 1) * 4; // 세로 모서리
        res += cases2[0] * (N - 2) * 4; // 윗면 모서리
        return res;
    }
}

---

결론

---

주사위의 가능한 모든 경우를 생각해보면 쉽게 해결할 수 있는 문제!

---