문제
https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
해설
해당 문제는 11659 구간 합 구하기 4번 문제와 유사하지만,
2차원으로 확장된 문제이다.
아래의 그림을 통해 이를 이해해보자.
연두색의 면적을 구하고 싶을때는 어떻게 해야할지를 예시로 들어보자.

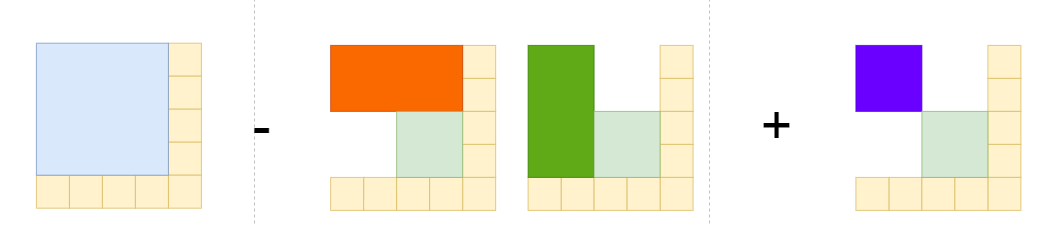
연두색 면적을 구하기 위해서 파란색 부분에서 주황색, 초록색을 빼고, 보라색 면적이 두번 빼졌으므로,
보라색 부분을 한번 더해주면, 연두색 면적이 나오는 것을 알 수 있다.
이러한 방식을 통해 2차원의 누적합 문제를 해결할 수 있을 것이다.
그렇다면, 누적합은 어떻게 구해야할지 생각해보아야 한다.
현재 상태에서 파란색의 누적합을 구하려면 아래와 같이 구해야 한다.
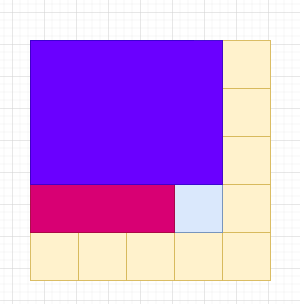

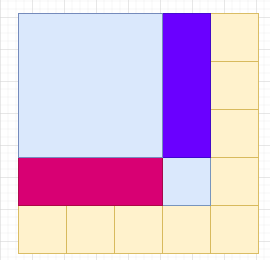
보라색 면적과 자주색 면적을 빼고 중복되는 부분인 파란색 부분(중복되어 뺀값과 자기 자신 값)을 더해주면 된다.
이제 코드를 통해 해당 알고리즘을 구현해보자.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int arr[][] = new int[N][N];
int sum[][] = new int[N+1][N+1];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + arr[i - 1][j - 1];
}
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int res = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1];
sb.append(res).append("\n");
}
bw.write(sb.toString());
bw.flush();
bw.close();
}
}- 2차원배열에 대한 누적합을 sum[i][j - 1] + sum[i - 1][j] + arr[i - 1][j - 1]을 통해 구해준다.
- 계산된 누적합에 대해서 sum[x2][y1-1] 과 sum[x1-1][y2]를 빼고 두 영역에 중복되는 부분인
sum[x1 - 1][y1 - 1]을 더해주면 계산할 수 있다.
결론
누적합을 2차원으로 생각했을 때 어떻게 될지 몰라서 찾아보니 정말 가로와 세로가 있는 2차원 평면에서
사각형의 넓이를 구한다고 생각하니 이해하기가 수월했던 것 같다.!
'CodingTest > 백준' 카테고리의 다른 글
| [백준] 그리디 알고리즘 (11047 : 동전 0) (0) | 2023.10.22 |
|---|---|
| [백준] 누적합 (25682 : 체스판 다시 칠하기2) (0) | 2023.10.21 |
| [백준] 누적합 (16139 : 인간-컴퓨터 상호작용) (0) | 2023.10.20 |
| [백준] 누적합 (2559 : 수열) (0) | 2023.10.19 |
| [백준] 누적합 (11659 : 구간 합 구하기 4) (0) | 2023.10.19 |
